数学が苦手な人は社会の仕組みがわかってない

私たちは毎日さまざまな計算の世話になっている（写真：metamorworks／iStock）

高校時代の数学の授業風景が思い浮かぶ。

先生をぼんやり眺める自分。電子黒板にはたくさんの数式と、何本かの接線を持つ山型のグラフ──。高校で数学を選択した人なら誰でもそうだろうが、公式やグラフの使い方は丸暗記するしかなかった。

私は数学の哲学者で、数学の成り立ちと、人間が数学をどうやって身につけるかについて考えている。この立場から、仕事で必要かどうかには関係なく、数学の実際的な価値はとても大きいことを理解している。

拙著『公式より大切な「数学」の話をしよう』でも詳しく書いているが、数学は現代の社会で重要な役割を果たしている。数学は、多くの人が思うほど無意味で不可解なものではない。むしろその逆なのだ。

数学は公式だけで片づけられるものではない。具体的な計算が求められるときに公式は便利だが、それに頼るあまり、ベースとなる考え方の理解がおろそかになってしまうこともよくあるからだ。

数学のなかには、驚くほど応用範囲が広く、誰でもたやすく理解できる分野がある。数式を使わずに説明できれば、さらにとっつきやすい。例えば、グラフ理論。グーグルなどの検索エンジンでは検索結果の順位づけに使われるが、がん患者の治療効果を予測したり、都市の交通状況を把握したりするためにも、同じ理論が役立てられている。

Netflixの「マッチ度」

映像をストリーミング配信するNetflixでも、グラフ理論が活用されている。作品ごとに緑色で示されている数字は、ふだん見ている作品との「マッチ度」だ。マッチ度が高いので気に入ると思って視聴したのに、まったくおもしろくなかった、ということもたまにある。

しかし、この数字をそれなりに信用してマッチ度の高い作品を選んでいくと、好きな映画やドラマの傾向がはっきりしてきてハズレが少なくなるはずだ。マッチ度は、新たな作品を視聴するたびに自動的に更新される。つまりコンピューターのプログラムで、ユーザーの好みに合う作品かどうかを判断しているわけで、作品の良しあしを評価しているわけではない。

基本的な考え方はとても単純で、「よいオススメ」とは、本人が「見て」気に入っている作品に似たものであるということだ。Netflixでは、世界じゅうの会員が「こちらもオススメ」にあげられた（つまり視聴済みの作品とのマッチ度が高い）作品を見ている。

映画が2作あったとして、片方を見た後でもう1作を見る人が多ければ、その2作は似ているとみなせる。例えば「アイアンマン」のあとで「アイアンマン2」を見た人がとても多いなら、この2本は似ているに違いないので、「アイアンマン2」は「アイアンマン」を見た人にとって「よいオススメ」と言える。Netflixを利用する人が多いほど、レコメンド機能の精度も上がる。コンピューターで、特定のユーザーと視聴履歴の似ている人がすでに見た作品を選び出せるからだ。

映画1本、ドラマ1作品をそれぞれ1個の円で示すとする。そのような図を使って計算を進めるには、円と円を結ぶ線ごとに数値が明らかでなければならない。ここでの数値は、クリックした作品を両方とも見た人の数だ。3作の映画だとすると、次の図のようになる。

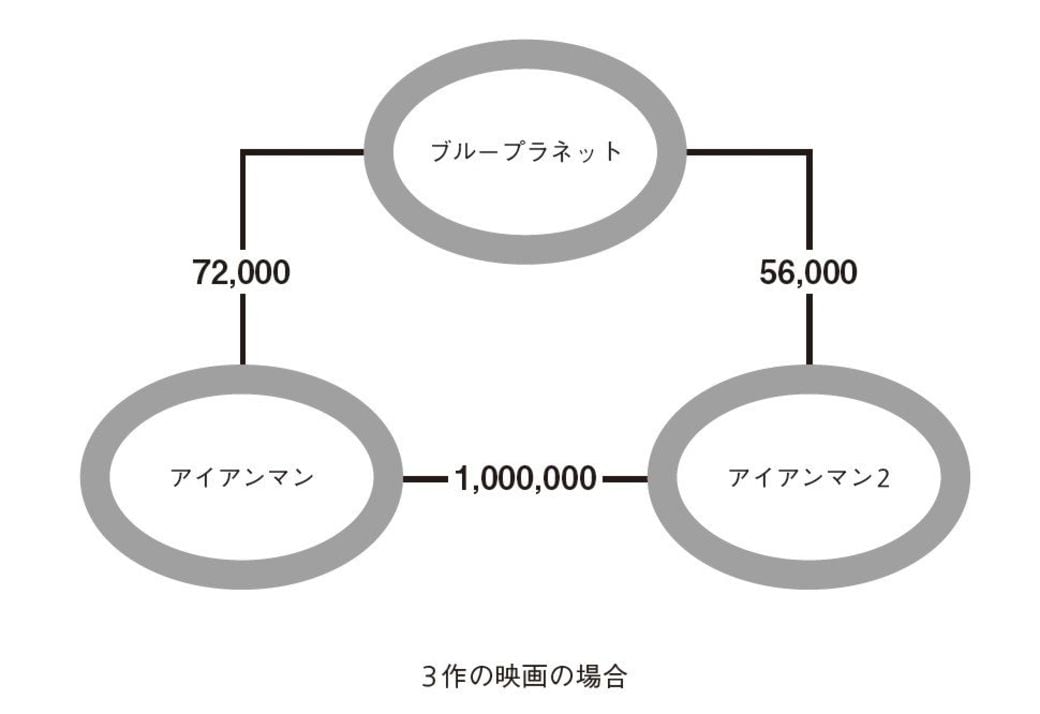
（外部配信先では図や表を全部閲覧できない場合があります。その際は東洋経済オンライン内でお読みください）

この図から、ユーザーの好みと各作品のマッチ度がどうなるかを考えてみよう。あるユーザーがNetflixで「アイアンマン」だけを見ていたとする。そのときコンピューターの仕事は、このユーザーが「アイアンマン2」と「ブループラネット」をそれぞれどの程度気に入るかを予想することだ。図の数字からすると、「アイアンマン2」のマッチ度は相当高くなる。好みが同じユーザーの多くが見ている作品であれば、「よいオススメ」、つまり気に入る可能性が高い。